Making decisions, the Decision Tree analysis method
Making decisions can be tricky, especially when there are many different possible choices and outcomes. One tool that may assist you in this process is a Decision Tree.
| A Decision Tree is a graphic representation to visualise different choices, with a probability analysis to calculate the overall expected value of the project. |
A decision tree is a structured approach to the decision making process, where a decision maker can investigate the outcomes of an uncertain choice. They help to form a balanced picture of the risks and rewards associated with an event.. Outcomes and probabilities are shown on a flowchart that resembles tree branches, where results are summed over time to an expected value. The option with the highest expected value is the prefered choice. It should be noted that obtaining useful estimates about probabilities is extremely difficult (especially if using gathered data), and the quality of the information will reflect the quality of the outcome.
Drawing a Decision Tree
You start a Decision Tree with a decision that you need to make. Draw a small square to represent this towards the left of a large piece of paper.
From this box, draw out lines towards the right for each possible option, and write that option along the line. Keep the lines apart as far as possible so that you can expand your thoughts.
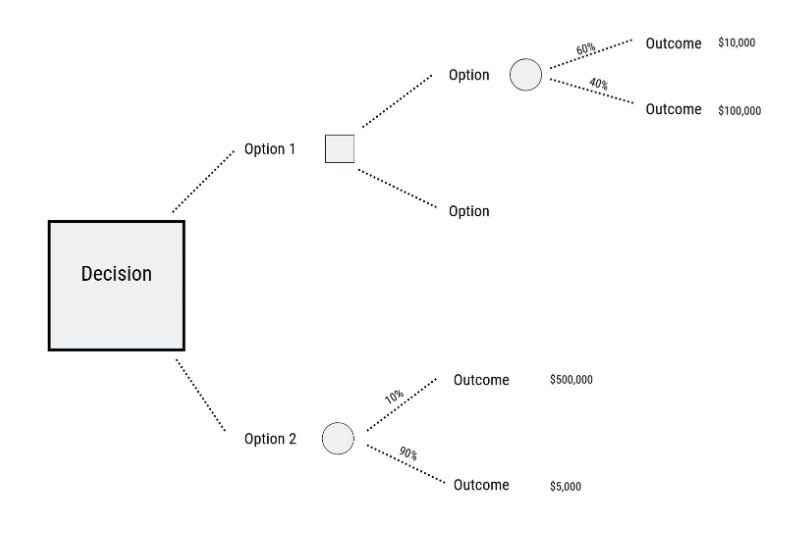
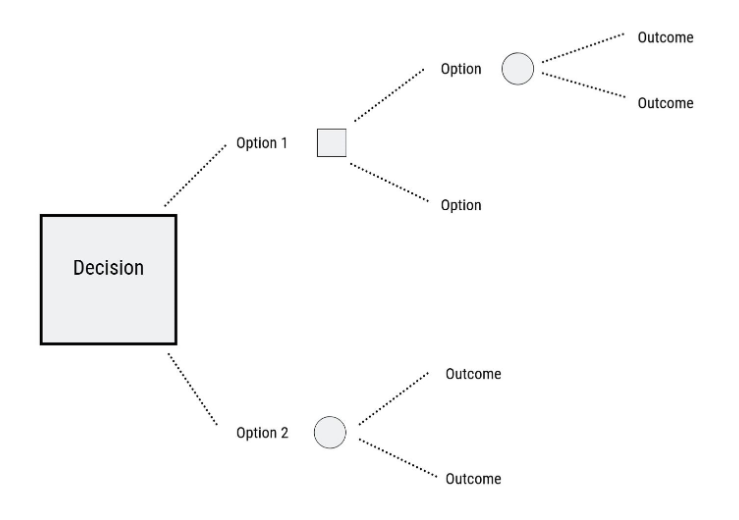
At the end of each line, consider the results. If the result of taking that decision is uncertain, draw a small circle. If the result is another decision that you need to make, draw another square. Squares represent decisions, and circles represent uncertain outcomes. Write the decision or factor above the square or circle. If you have completed the option at the end of the line, just leave it blank.
Starting from the new decision squares on your diagram, draw out lines representing the options that you could select. From the circles draw lines representing possible outcomes. Again make a brief note on the line saying what it means. Keep on doing this until you have drawn out as many of the possible outcomes and decisions as you can see leading on from the original decisions.
Once you have done this, review your tree diagram. Challenge each square and circle to see if there are any options or outcomes you have not considered. If there are, draw them in. If necessary, redraft your tree if parts of it are too congested or untidy. If you have compiled a comprehensive list of probable outcomes then the model will be significantly compromised.
Evaluating your Decision Tree
Now you are ready to evaluate the decision tree. This is where you can work out which option has the greatest worth to you. Start by assigning a cash value or score to each possible outcome – how much you think it would be worth to you if that outcome came about.
Next look at each circle (representing an uncertainty point) and estimate the probability of each outcome. If you use percentages, the total must come to 100% at each circle. If you use fractions, these must add up to 1. If you have data on past events you may be able to make rigorous estimates of the probabilities. Otherwise write down your best guess.
Calculating Tree Values
Once you have worked out the value of the outcomes, and have assessed the probability of the outcomes of uncertainty, it is time to start calculating the values that will help you make your decision.
Start on the right hand side of the decision tree, and work back towards the left. As you complete a set of calculations on a node (decision square or uncertainty circle), all you need to do is to record the results. You can ignore all the calculations that lead to that result from then.
Calculating the Value of Uncertain Outcome Nodes
Where you are calculating the value of uncertain outcomes (circles on the diagram), do this by multiplying the value of the outcomes by their probability. The total for that node of the tree is the total of these values.
Calculating the Value of Decision Nodes
When you are evaluating a decision node, write down the cost of each option along each decision line. Then subtract the cost from the outcome value that you have already calculated. This will give you a value that represents the benefit of that decision.
Note that amounts already spent do not count for this analysis – these are ‘sunk costs’ and (despite emotional counter-arguments) should not be factored into the decision.
When you have calculated the decision benefits, choose the option that has the largest benefit, and take that as the decision made. This is the value of that decision node.
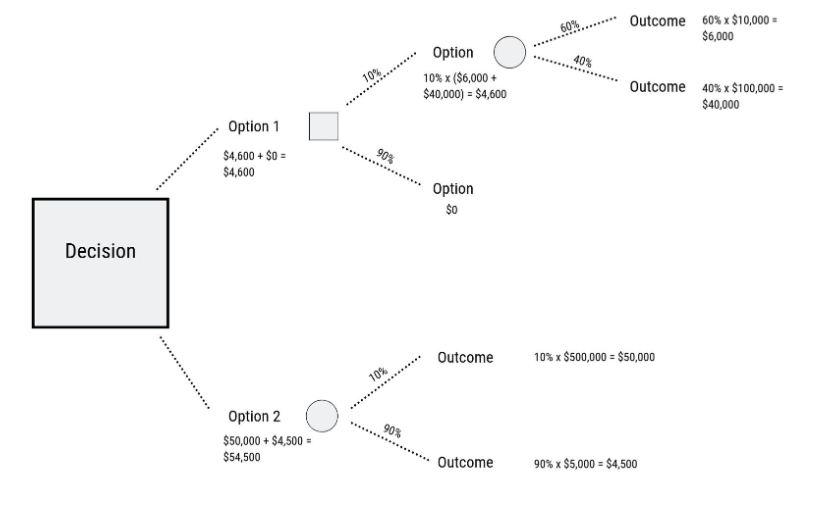
Example – sowing canola or wheat
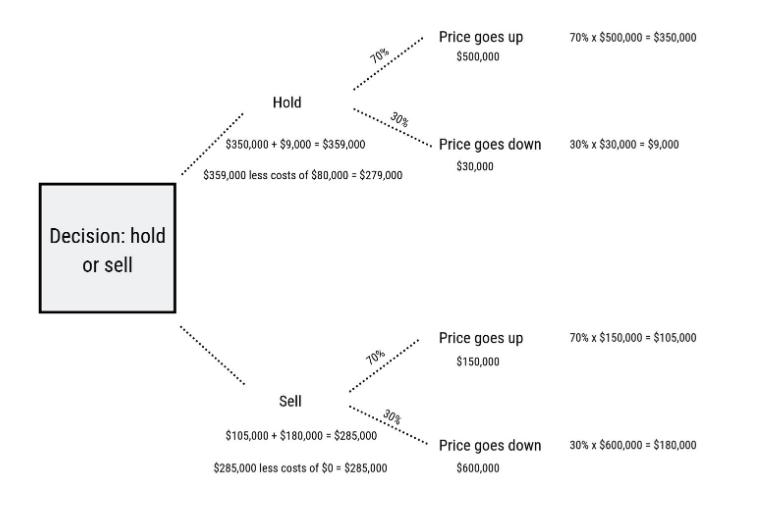
Below is an example of how the Decision Tree could be used. In this example the decision needs to be made whether to hold or sell.
In this example, the benefit we calculated for ‘hold’ was $359,000. We estimate the future cost of this approach as $80,000. This gives a net benefit of $279,000.
The net benefit of ‘sell’ was $285,000, with a future cost of $0. Giving a benefit of $285,000.
Given this analysis the preferable option at this moment in time is to sell.
Key points:
Decision trees provide an effective method of decision-making because they:
- clearly lay out the problem so that all options can be challenged
- allow us to analyse fully the possible consequences of a decision
- provide a framework to quantify the values of outcomes and the probabilities of achieving them
- help us to make the best decisions on the basis of existing information and best guesses.
- Obtaining a comprehensive list of probable outcomes is very important
- Poor input = poor output
As with all decision-making methods, decision tree analysis should be used in conjunction with common sense – decision trees are just one important part of your decision-making tool kit.
Further Information
Avoid sunk cost interfering with your decisions – Economic Video Series
![]()

One comment, add yours.
Stephen Orchid
I want to express my gratitude to this writer who writes very well and covers all the information on the topic. I have never read this information before. This is really an amazing topic which means a lot.